As the three or four readers of my missives know, one of my big concerns is “What sort of questions can we ask our students in the internet era?”
So today, let’s talk about throwing axes:
Now you might wonder what this has to do with math. The answer should be obvious: Some people are born with “axe arms.” They instinctively know how to throw axes. It’s why people say “I’m just bad at throwing axes,” and when you try to teach them, they’ll say “When am I ever going to use this?” (and they’re not convinced when you say “Suppose there’s a zombie apocalypse and you need to throw an axe…”).
No, wait, wrong script.
I got good because…wait for it…I practiced.
OK, that should be obvious. And it’s something we always tell our students: You won’t get good unless you practice, so here’s 25 problems to practice on.
This works up to a point, but sooner or later runs into a fundamental problem: human beings are intelligent, and intelligent beings get bored doing the same thing over and over again.
Say I give a student 25 linear equations to solve. They may struggle with the first five. But by the second five, they’ve started to figure things out. And the third set of five they’re in the groove.
At that point, boredom kicks in, because they realize they’re doing the same thing, over and over again. So they start to make mistakes, not because they don’t know what they’re doing, but because they’re not paying attention. Those last ten problems will be increasingly riddled with simple errors.
And now for the really bad news: what they’ve practiced in those last ten problems, and what they’ll most likely remember from the assignment, is how to solve the problem incorrectly.
How can we avoid this? Let’s get back to throwing axes. I practice, but I don’t just stand at the throwing line and try to hit the target. Once I’ve established that I can hit the target reliably, I take a step back and try to hit the target, which is now a little further away. And once I can reliably hit the farther target, I take another step back and repeat the process.
In other words: You acquire skill by tackling increasingly difficult tasks.
I call this “shifting the lines.” To begin with, we can change the starting line. This is more comfortable for students: they know what the goal is, and the idea that they’re starting a little farther away isn’t too daunting.
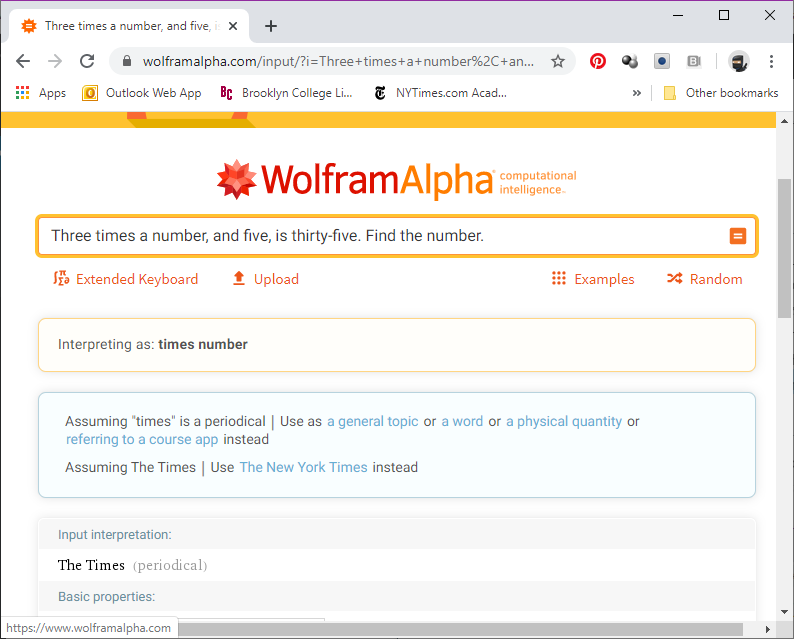
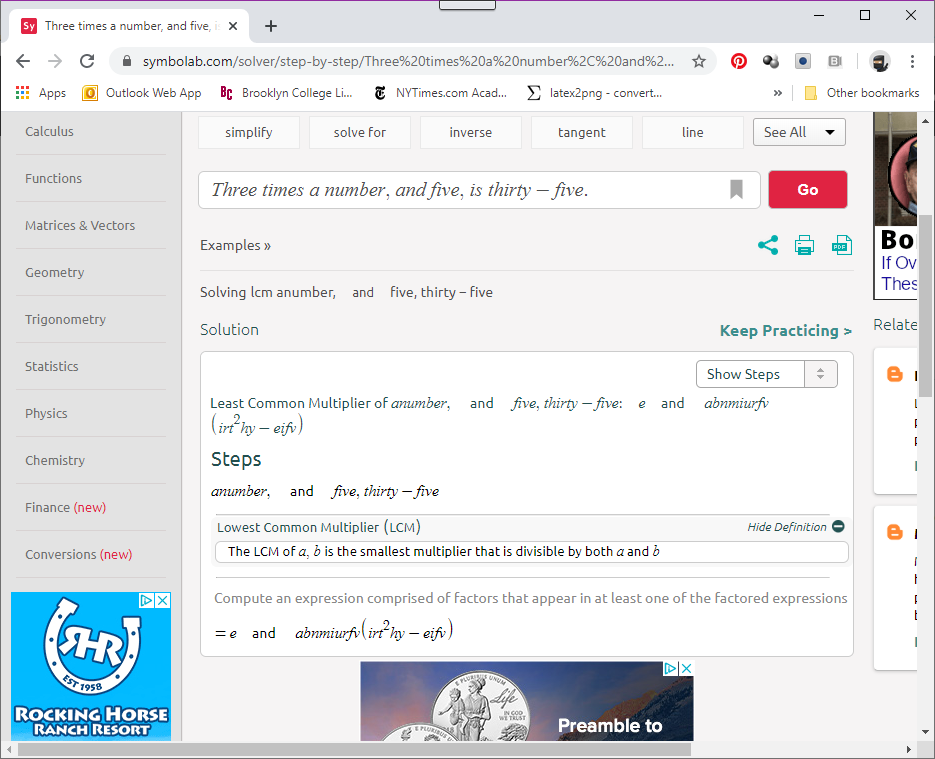
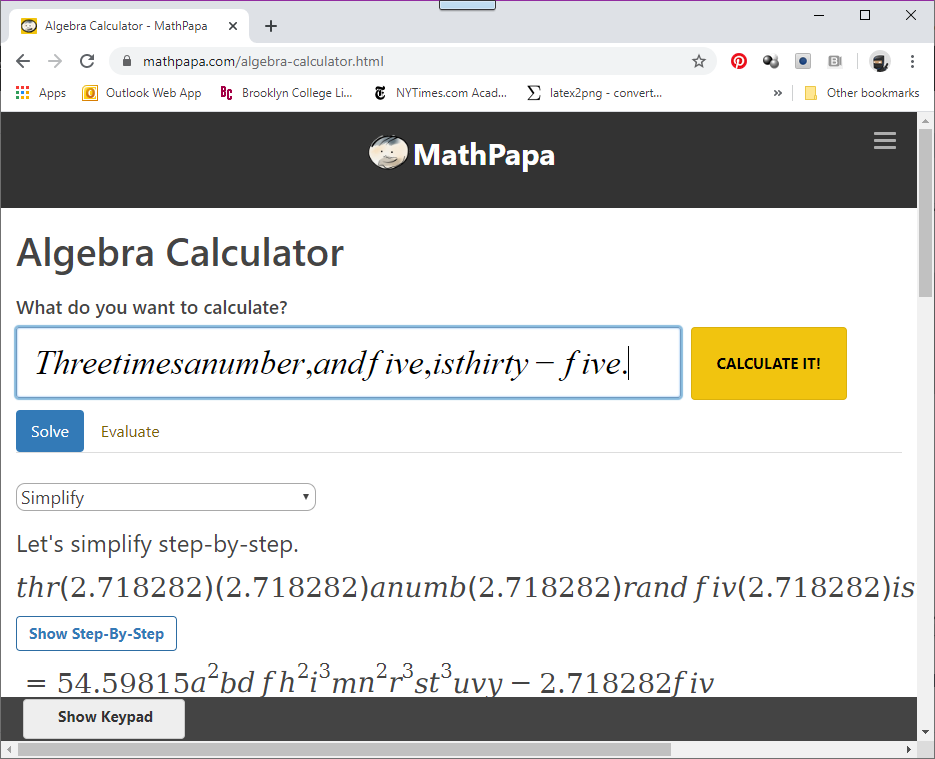
So let’s consider those linear equations again: “Solve 3x + 5 = 25.” It’s easy enough to come up with five or so problems like this, and students can practice. However, it’s just as easy for students to run the problem through an online calculator and get the answer, with all steps shown. Consequently, this type of question is meaningless for an exam: it fails to distinguish between the students who “know how” to solve the problem, and the students who can use an online calculator.
But move the starting line. Where might such a problem come from? Typically, these come from word problems. So wrap these linear equations with some words: “The width of a rectangle is 5 feet longer than three times the length. If the width is 25, what’s the length?” This type of problem will produce nonsense results when run through an online calculator, so it’s a far better question to ask.
Notice that this question places a premium on the ability to translate a written statement into a mathematical one. While this is a worthy goal, once the student realizes the problem is “Solve 3x + 5 = 25”, they can run that through an online calculator. Arguably, that’s not a problem: it’s a proper division of labor, with the human doing human things (reading and interpreting) and the machine doing machine things (mindless application of an algorithm). But maybe we want more.
The problem here is that the question gives us an equation to solve: “The width is 25.” Since solving equations is the epitome of an algorithmic process, it’s exactly the type of thing computers are good at. So if we want to internet proof our questions, the answer cannot be the solution to an equation.
So let’s move the finish line. Solving our equation gives us the length. If the length isn’t the answer, why are we finding it? Maybe we need to find the area. So change the problem: “The width of a rectangle is five feet longer than three times the length. If the width is twenty-five feet, what’s the area?”
Now we have a problem that’s internet resistant. Providing a correct answer requires identifying an equation to be solved; solving it; then using the solution to answer the question. Of these, only the middle step can be done by machine; the others require human intervention.
So here’s a general framework for writing questions in the internet era: If you want to ask a question but it’s something that can be run through a problem solver, shift the lines. Change the starting point, so a problem solver can’t solve it. And change the ending point, so that even with a problem solver, there’s much that a human must do.